MAN Wiki
Stereophonic (Rev #2, changes)

Showing changes from revision #1 to #2: Added | Removed | Changed

Stereo microphone systems ¹

A-B (delay-based)

A-B microphone system uses two parallel omnidirectional? microphones with a clear distance.

X-Y Blumlein pair and X-Y stereo in general (intensity-based, coincident)

Blumlein pair uses the setup of 90 angled crossed figure-of-eights microphones. According to Michael Gerzon, the Blumlein pair system has a most remarkable stereo stability.

A classic Blumleinian coincident microphone pair uses two figure-of-eight microphones pointing to $\pm 45 ^\circ$, in other words, two microphones are positioned $90^\circ$ from each other.

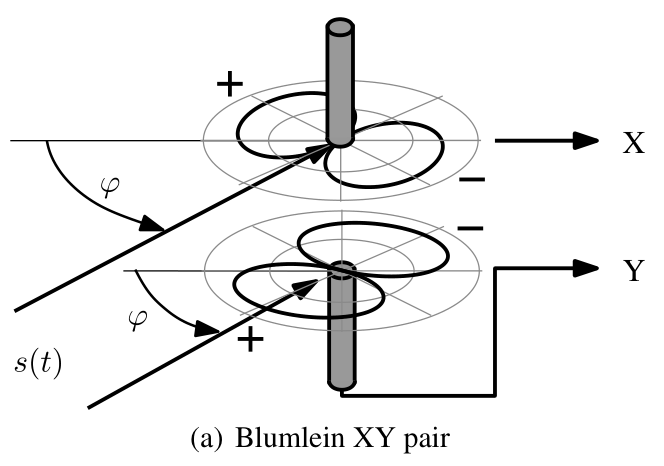
The pickup pattern of a classic Blumleinian microphone pair can be defined as:

where $\varphi$ is the angle of the sound source relative to the microphone pair, $g(\varphi)$ is the response of the Blumlein microphone pair to sound signals at different angles of incidence $\varphi$, and $X$ represents the front-right signal, while $Y$ represents the front-left one.

Assuming a signal $s$ originates from an angle of $\varphi$, the pickup signals’s gain can be expressed as:

As the sound source moves from the right channel $X$ at an angle of $-45^\circ$ to the left channel $Y$ at an angle of $+45^\circ$, the captured signal would be panned from the channel $X$ to the channel $Y$, the transition can be represented as follows:

Sound comes from the sides that have angles $\varphi$ ranged from $-135^\circ$ to $-45^\circ$ and certainly also $45^\circ$ to $135^\circ$ will make a Blumleinian microphone pair producing out-of-phase signals between $X$ and $Y$ channels.

Compared to a A-B way of setup, the sonic characteristic of a Blumleinian microphone pair has less sense of space and depth.

ORTF: (near-coincident)

ORTF (Office de Radiodiffusion Télévision Française) is a variation on the basic X-Y coincident technique, which uses two cardioid microphones spaced 7 inches (17 cm) apart and facing outward with an angle of $110^\circ$ between them.

M-S: (intensity-based)

The M/S technique employs a mid (omnidirectional?, sometimes cardioid?-directional to front) cartridge that directly picks up the mono sum signal, and a side (figure-of-eight) cartridge that directly picks up the stereo difference signal.

A native MS recording pair uses a pair of omnidirectional microphone (mid, $W$) and figure-of-eight microphone (side, $Y$).

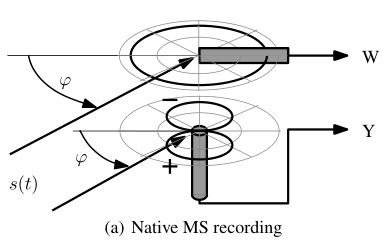
The pickup pattern of this MS microphone pair can be defined as:

where $\varphi$ is the angle of the sound source relative to the microphone pair, $g(\varphi)$ is the response of the MS microphone pair to sound signals at different angles of incidence $\varphi$, and $W$ represents the mid signal, while $Y$ represents the side signal.

Assuming a signal $s$ originates from an angle of $\varphi$, the pickup signals’ gain can be expressed as:

External resource

• https://www.michaelgerzonphotos.org.uk/
• SCHOEPS Double MS Plugin (Plug in for dematrixing double MS recordings): https://tonsturm.com/product/schoeps-double-ms

References

[1] Zotter, Franz & Frank, Matthias. (2019). Ambisonics: A Practical 3D Audio Theory for Recording, Studio Production, Sound Reinforcement, and Virtual Reality. 10.1007/978-3-030-17207-7. Download: https://link.springer.com/content/pdf/10.1007/978-3-030-17207-7.pdf

[2] Ballou, G. (Ed.). (2009). Electroacoustic Devices: Microphones and Loudspeakers (1st ed.). Routledge. https://doi.org/10.4324/9780240812687